Check your answers and understanding by reading through this Answer Set.

1. A table of data reports that a copper atom has an atomic radius of 140 pm.

a). What is the diameter of the copper atom in pm?

The diameter is double the radius, so 2 x 140 = 280 pm.

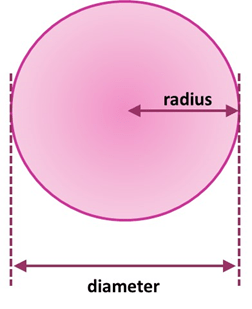
b). What is the diameter of the copper atom in nm?

1 pm = 10^-12 m and 1 nm = 10^-9 m.

This means that 1 nm = 1000 pm.

Hence, to convert the diameter from pm into nm we divide by 1000.

Diameter of a copper atom = (280 / 1000) nm = 0.28 nm.

c). What is the diameter of the copper atom in m?

Since 1 m = 10¹² pm, to convert the diameter from pm to m we divide by 10¹².

Diameter in m = (280 / 10¹²) = 2.80 x 10^-10 m.

d). The thin edge of a coin is 1.85 mm in thickness. Assuming it is entirely made from copper, how many atoms lined up end-to-end would fit across the coin edge?

Since we now have the diameter of a copper atom in m it makes sense to convert the dimension of the coin into m also:

1 m = 1000 mm, so we need to divide the 1.85 mm by 1000 to convert to m.

This gives coin thickness = 1.85 x 10^-3 m.

Finally, we can calculate how many atoms fit across the edge of the coin by dividing the thickness by the diameter of each atom.

Hence, number of atoms = (1.85 x 10^-3) / (2.80 x 10^-10)

Number of atoms = 6, 607, 143

This is over six and a half million atoms!

e). If 5.67 x 10⁶ nickel atoms would fit across the same coin edge. What is their radius in pm?

There are two ways of answering this question:

i) A similar process to the question above, starting with dividing the coin thickness by 5.67 x 10⁶ to get the diameter of one nickel atom in m. This can then be converted to pm by multiplying by 10¹² and finally, dividing the diameter by 2 to get the radius. This gives a value of 163 pm.

ii) Find the ratio of the number of copper atoms to the number of nickel atoms – this must be the same as the ratio of the nickel radius to the copper radius (since a larger diameter would require fewer atoms to cover the same distance). The working is shown below, I have rounded the answer to part d) and used the value of the copper radius in pm given at the start of the question.

2. An aluminium needle has a thickness equivalent to
2.72 x 10⁶ aluminium atoms laid end-to-end. What is the thickness of the needle in metres if an aluminium atom has a radius of 0.184 nm?

3. A potassium atom has radius of 2.75 Å, whereas a selenium atom has a radius of 0.190 nm – which is larger?

4. a. A gold atom has an atomic radius of 166 pm. Convert this distance into m.

b. Using the value in 4.a. calculate the volume of the gold atom in m³ if the volume of a sphere is given by this equation:

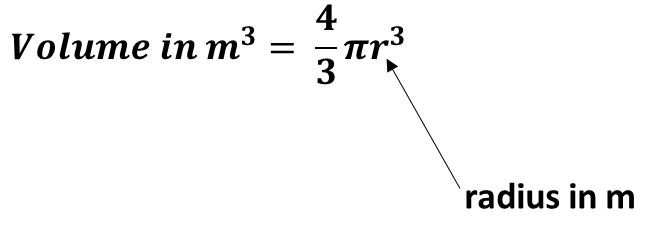
c. If atoms are imagined as spheres, it is not possible to stack lots of them together without any space being left in between them. Only 74% of the volume of an object can be occupied by atoms.

Calculate how many atoms must be in a flake of gold foil if the foil is 1 cm² and has a thickness of 0.0001 m.

5. a. A small copper coin has a mass of 3.56 g. If there are
3.37 x 10²² copper atoms in the coin, what is the mass of one copper atom in g?

b. Copper atoms have a relative atomic mass of 63.5 whereas iron atoms have a relative atomic mass of 55.8. How many iron atoms would be needed to give a coin of the same overall mass?

“Copyright Simon Colebrooke 26th March 2025”